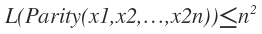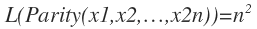モノトーンそしてmP≠mNP その3

おはようございます。大学は宮崎の大学に通ったのですが、日本も南の方に行けば行くほど時間にはだいたいでして、あちらには日向時間というものが存在しました。だからいつだってじれったかったりするのですが、慣れればそれが良かったりすると言う恐るべきもの。ちゃわちゃわっていう女の子の方言もかわいかったですね。もちろん熊本弁もかわいいですが。何処に行ってもその地方の女の子の方言の語尾ってかわいくて味がありますよね。


さて、今回から少しずつmP≠mNPを説明していくことになります。この結果はテキストによるとA.RazborovとA.E. Andreevがほとんど同時に独立に証明したものである、とあります。

【定理】
　1<K≦n^(1/4)とするときClique k,nを表わすモノトーンサーキットのサイズは少なくても

　　　　

  ※註　当然のことながら、ここでf(n)=Ω(g(n))は、c>0なる実数が存在していればf(n)≧c・g(n)となるような関数


【証明の方針】
もしサーキットサイズが小さければ、そのサーキットはだいたいの肯定テストグラフに0の値を与えたいていの否定テストグラフには1値を与えることをいう


以上のようなやり方でやっていくのですが、詳細は追々説明するにしても、これがいくつもの補題があるのでややこしいです。

さて、だいたいの、ということがありましたが、考え方としてまず肯定的テストグラフであるか否定テストグラフであるかどうかの判断はn個のノードがある場合k個のノードかk-1個のノードのクリークがあるかどうかを判定してから詳細に判断すればいいわけで、そういう考え方の元、以下にクリーク表示というものを定義します。

【クリーク表示の定義】
　グラフGのノード集合Xがあったときに、これがクリークになっているときに、
　
　 ┌X┐(G)=1

そうでないときには

　 ┌X┐(G)=0

と┌X┐を定義してクリーク表示と言うことにします


また、クリーク表示を用いて近似サーキットというものを考えます。まず定義の方針としては、高々m個のクリーク表示を∨で結んだもの、すなわち┌X1┐∨┌X2┐∨…∨┌Xr┐でr≦m、またさらに|Xi|≦lがすべてのi=1,…,rに対して成立しているものとします。ただしm≧2かつl≧２です。さて元のサーキットのノード数nやいくつのノードのクリークであるかを示すkにk関する制限は後ほど述べていくことにして、モノトーン・サーキットCを近似サーキットC'にする場合の定義の条件というものを記しておきましょう。

【近似サーキットを定義する際の条件】
　1．Cが小さいモノトーン・サーキットならば、たいていの肯定的テストグラフGについて
　　
　　　　C(G)≦C'(G)

　　が成立している。

　　さらに、たいていの否定テストグラフGでは

　　　　C(G)≧C'(G)

　　が成立している。

すなわち、近似サーキットの方が肯定テストグラフにおいては成立するものが多く、否定的テストグラフの方では元のサーキットの方が成立するものが多いという事ですが、証明の方針に従って

　2．すべての近似サーキットは、たいていの肯定的テストグラフに0の値を与えるか、またはたいていの否定的テストグラフに1を与えるかのどちらかである

という条件も加えます

次回は、この近似テストグラフをリーフから順に定義していきます。

モノトーンそしてmP≠mNP その2

おはようございます。何故か休みの日の朝が一番しんどいという気がするのですが何故でしょうか。そうです、それはこのブログの記事をを書かないといけないから……。え、あ、なぜか、またしーんとしちゃって……。え、あの、もとい、その前の日にしっかりと仕事をがんばってきているからです。ええ、多分、そうです。いや、多分、そうに違いありません。


さて、今回は引き続き定義となります。

前回は言語Lやpredicate Pがモノトーンであるとはどういうことかと言うことを定義しました。今回はそれらがクラスmNPやクラスmPに属することがどういうことかということについて定義していきます。

【クラスmNPに属するという事の定義】

• 言語LがmNPに属することをLがモノトーンであってさらにNPに属することとする
• predicate PがmNPに属することも同様にpredicate PがモノトーンであってさらにNPに属することとする

【クラスmPに属するという事の定義】

• 言語LがmPに属することをLが多項式サイズのユニフォームなモノトーン・サーキットで表わされることとする
• predicate PがmNPに属することも同様にpredicate Pが多項式サイズのユニフォームなモノトーン・サーキットで表わされることとする
  ※ここでモノトーン・サーキットとはリーフのブール変数がx1,x2,…,xnで表わされ、￢x1,￢x2,…,￢xnではないということ

さてこのほかに問題を扱う上で重要となるのが、predicate Pの扱いですが、すべての言語は自然数にコーディングできます。このコーディングした自然数を二進法で{0,1}*に変換した上で、その二進法での{0,1}*のpredicateがmPかmNPかであるかという判断をすると定義しておきます。ここはちょっと難しいですが、前回と合わせてよく考えてみて下さいね。


さて、ここまでが前提としての定義ですが、もう少し、今回の証明に必要な定義を予めやっておこうと思います。

「頂点カバー、独立セット、クリーク　その１」で頂点カバーやクリークというサーキットの問題を説明し、以下、これら三つが同等でNP完全（「頂点カバー問題がNP完全であるということ　その１」～「その４」）であるという話をさせて頂いていますが、今回このうちクリーク問題を使って考えます。


【Clique k,n(G)、肯定的テストグラフ・否定的テストグラフの定義】

そこで、Clique k,n(G)を、Gはn個のノードをもつグラフで、そこにk個のノードによるクリークが存在するかを決定する問題とします。存在すればClique k,n(G)=1、しなければClique k,n(G)=0となります

また、このときn個のノードを持つグラフが肯定的テストグラフであるということを、k個のノードのクリークを持っていて、それ以外の枝を一つも持っていないとします。肯定的テストグラフであれば、すなわちClique k,n(G)=1であることは自明です。またn個のノードからk個のノードを取ってくる組み合わせですので、nCm個の肯定的テストグラフが存在します。

同様に、n個のノードを持つグラフが否定的テストグラフであるということを、n個すべてのノードに1～k-1の値のうちどれか一つを振り当て、異なった値を持つ二つの頂点だけが辺で結ばれているグラフと定義します。否定的テストグラフであれば、すなわちClique k,n(G)=0です。またn個のノードに1～k-1の値を振り当てる組み合わせは(k-1)^n通りあります。否定的テストグラフのノードに与える値の組み合わせが違ってもグラフの形が同じだという場合もありますが、これはすべて違うグラフと見なすということにします。



以上を予備的な定義としまして、他にもう少し近似サーキットの定義などもありますが、これは、次回以降、mP≠mNPを示す定理とその証明の説明の中でしていくことにします。

モノトーンそしてmP≠mNP その1

おはようございます。今日から新章に入ります。そう言えば新米の季節ですね。おいしい新米。うれしい新米。楽しい新米。まだまだ新米（？）の私ですが宜しくお願いいたします。ちょっと嘘が入ってますかね。ええ、分っています。新米ってほどでもないって事ですよね。


さて、この章ではモノトーンのサーキットを検討していきます。思い出して頂きたいのですがこの章で言うモノトーンは「サーキットというグラフの計算量　その１」などで出てきていて、

　　　x≦y　　ならば　f(x)≦f(y)
　　　
　　ただし、x=(x1,x2,…,xn),y=(y1,y2,…,yn)で、
　　　　　　x≦yはx1≦y1∧x2≦y2∧…∧xn≦yn
　　　　　　を意味します
　
となっています。

では、本題に入り、まず今回と次回は定義をいくつか述べます。今回はモントーンな関数fや言語L、そしてクラスPの表記の一種predicate Pのモノトーンについて定義します。ただし、この章でも特に断らない限り^はべき乗を表わす二項演算子であるとします。

【モノトーンな関数ｆや言語Ｌやpredicate Pの表記によるモノトーンなクラスPの定義】

　ブール関数fがf:{0,1}^n→{0,1}、即ちこれをn個の二進数の元を持つ集合から0か1かへの2値への写像であるとする場合、fを言語

　　L={x|x∈{0,1}^nでf(x)=1}

で表わすこととします。また同時にfをクラスPのブール変数x1,x2,…,xnのpredicate P（predicateは日本語で述語の意味）とい表記の仕方で表わすときは

　P(x1,x2,…,xn)　iff　f(x1,x2,…,xn)=1

という定義になります。

さて、fがモノトーンであるとします。このとき、Ｌやpredicate Pもモノトーンとなります。

すなわち、Lのモノトーンとは

　(x1,x2,…,xn)∈L,(x1,x2,…,xn)≦(y1,y2,…,yn)→ (y1,y2,…,yn)∈L

となります。同様にpredicate Pがモノトーンであるということは

 P(x1,x2,…,xn),(x1,x2,…,xn)≦(y1,y2,…,yn)→ P(y1,y2,…,yn)
　
が成立するということです。ちょっとややこしいので今回はとりあえずここまでにしましょう。

サーキットの計算量の様々なクラス その9

おはようございます。10月ももうすぐ終わり。そうしている間にあっという間に一年も終わりそうですね。落ち葉の季節も近づきましたが、こちらも大詰め。しかしもう少しでゴールが見えてきそうで見えてこない。ちょうど十月終わりといった状況であります。


今回、「サーキットの計算量の様々なクラス」と題して代表的なクラスの計算量の考え方についてその概要を説明してきました。これがどれほどの意味を持つのか難しく、クラスAとBにおいてのクラスの分類A≠Bという、あまり関係しないのではというのが竹内外史先生のご意見のようです。そういうこともあって、ここまである程度駆け足で見てきました。

これからの進め方ですが、計算量のクラスのお話しは今回でいったん終わり、次回からはモノトーンサーキットでの問題について説明したいと思います。こちらは、分っていることが多く、また、実際の電子回路などの設計にも応用できそうな手法が多く見受けられると言うこと、などがその理由です。

では本題に入ります。

前回クラスγ/Fを

　　　γ/F={L⊆{0,1}*|∃B∈γ,h∈F,L={x｜<x,h(|x|)>∈B}　　　　　

と定義するとき、γ=P、F=Polyの場合すなわちP/Polyが重要であり、定理としてP/Polyがノンユニフォーム多項式サイズのサーキットの表わすクラスであること、などをお話をしました。今回、サーキットの計算量の様々なクラスのお話しの最後として、補足説明的なお話しをいくつかさせて頂こうと思います。

やはり前回の最後に、

「単にPをユニフォームな多項式サイズのサーキットであると見なせる観点から、P/PolyをノンユニフォームPと呼ばれるとテキストにはあります。」

と述べましたが、これに関連して、P=NP問題を解く際、NP⊆Pを解くという方法の他に、

　　　NP⊆P/Poly　

という事の検討興味ある問題だとあります。ここで、P/PolyにはクラスPに入らないものはいくらでもあるためP/PolyがクラスNPに含まれないということは明らかであるために、NP=P/Polyと言わないともあります。たとえば、P/Polyのサーキットのサイズが多項式サイズであっても、結果を自己言及できないために真偽の判断をクラスNPでは判断できない、場合があると考えれば良いのではないでしょうか。

このことに関して、テキストもあまり詳しく触れておらず、ここまで説明を省略してきたTMを拡張したOTMやNOTMを含んだ階層構造、これをポリミナル・ハイアラーキー（PH）と呼びますがこれにも関係してくるという事などが簡単に触れられています。

このあたりの議論に関しては以下の論文などを参照すると良いようです。

「R.M.Karp and R.Lipton, Turing machines that take advice, Enseign.Math,28(1982),191-209.」

これに関連していくつかの数学基礎論的・計算機理論的「言語」も紹介されていますが、今回は省略します。最後にテキストのp.55からのこの節に関する最後の部分を引用して終わりたいと思います。

「　不思議なことに、以下の重大問題、いろいろなクラスA,BについてA≠Bを証明したいという議論の中で、このユニフォームの概念が用いられることはほとんどない。
　まだ学問が未発達で、それが関係する段階に到っていないのか、それとも本質的にクラスの分類A≠Bという問題には、ユニフォームという概念が関係しないのか？すなわち今まで考えられているクラスには、その分離の問題はユニフォームという性質とは独立の問題なのかは分らない。
　しかし著者は後者の方の意見に傾いている。」

サーキットの計算量の様々なクラス その8

おはようございます。いかに失うものもないタコのようなふにゃふにゃのしている私でも、いろいろ悲しいことはあります。しかし、生きているだけで必要にして十分であるはず。ええ、すでに何を言っているか自分でも分りませんが、さて、今回のことをきちんと説明できるのでしょうか。


前回クラスγ/Fを

　　　γ/F={L⊆{0,1}*|∃B∈γ,h∈F,L={x｜<x,h(|x|)>∈B}　　　　　①

と定義するとき、γ=P、F=Polyの場合すなわちP/Polyが重要であるというお話をしました。今回は、以下の定理を説明します。

【定理】　L∈P/Polyの必要十分条件は
　　

で定義されるブール関数の列fnが多項式サイズのサーキットで計算されることである。

すなわち、P/Polyがノンユニフォーム多項式サイズのサーキットの表わすクラスである

【証明】
(i)L∈P/Polyを仮定する

このときPに属するB（①式での∃B∈γの部分）とPolyに属するh（①式でのh∈Fの部分）で

　　　　L={x｜<x,h(|x|)>∈B}　

を満たすものがあるという事になります。以下n=|x|と表わすこととし、

　　　　m=|<x,h(n)>|

と定義すれば、多項式サイズのサーキットCmで


　　　　<x,h(|x|)>∈B　iff Cmは<x,h(|x|)>に対して1を計算する
　
　　　　　※iffは同値関係をあらわす


を満たすものが存在するという事になります。なぜなら、定義から「<x,y>はO(|x|+|y|)の時間でx,yが計算される」からです。(前回の記事を参照して下さい）

また、Cm以外のリーフがm個のサーキット全体C'nを考えても、mはnで押さえられており、かつ仮定からLはクラスPであり、Pであれば、前々回説明したように　多項式サイズのサーキットによって計算可能となるからです。従って、まず必要条件の証明が終わりました。


(ii)Lが多項式サイズのサーキットCnで決定されると仮定する

このCnをコーティングするようなh(n)があり、|h(n)|はnの多項式p(n)によって押さえられる、すなわち

　　　|h(n)|≦p(n)

であるとします。このことは、すなわち、h∈Polyである事を意味しますね。（前回のPolyの定義を参照して下さい）

一方仮定より、入力xと与えられたCnから出力が1か0かというのは多項式時間により決定できますから、クラスPであることは明らかです。このことをBとすると、

　　 x∈L　iff <x,|h(x)|>∈B

となりますので、L∈P/Polyが導かれ、十分条件が証明されました


単にPをユニフォームな多項式サイズのサーキットであると見なせる観点から、P/PolyをノンユニフォームPと呼ばれるとテキストにはあります。

次回はもう少し補足説明をして、今回のクラスの話を終えたいと思っています。しかし、もう少し説明することもあるかなとも考えていますので、現在少し悩んでいるところです。

サーキットの計算量の様々なクラス その7

おはようございます、ではなくすでに、こんにちはですね。いや、がんばっている分、眠くなる今回の記事。報われない思いがするのは私だけでしょうか。などと言いつつ、途中疲れて寝てしまったのも私。まったく反省しきりでございます。


さて今回から、ノンユニフォームの多項式サイズのサーキットを表わすクラスについて、以下数回にわたって考えていくことになります。

前回同様、注意点としてx^iという式の^はべき乗を表わす二項演算子とします。

今回は必要な定義についてです。いろいろ記号が出てきます。できるだけ解説を入れて説明したいと思いますが、「チューリングマシンの数理モデル」や「クラスPとチューリングマシンその１」などの記事もご参考頂ければ幸いです。


【関数集合Fの定義】
まず、Fをh:N→Σ*なる関数hの集合とします。ここで、Nは自然数全体の集合、Σ*は入力記号の全体の集合。従ってここではすべて自然数があればそれを入力全体の集合にするようなそのような関数をh、その集合をFとすると言い換えることができます。


【関数集合Polyの定義】
次に、Polyを定義して、|h(n)|がn（入力xとしたときの|x|）の多項式で押さえられているすべてのh:N→Σ*の関数の集合とします。


【関数集合γおよびγ/Fの定義】
γをL⊆{0,1}*なる言語Lのクラス、即ち、言語Lはすべての2進数全体の部分集合で、Lの中の集合（クラス）をγとしたときに

　　　　< , >:({0,1}*)^2→{0,1}*

が1対１の写像を表わす関数、言い換えれば、({0,1}*)^2を{0,1}*にへのコーディングであり

　　　　|<x,y>|=O(|x|+|y|)

を満たすものであるとする。ただし<x,y>はO(|x|+|y|)の時間でx,yが計算されるものとする。このような<,>の例はいくらでもありますね。

このとき、Fの助けを借りて、γから計算できるクラスγ/Fを次の式で定義するものとします。

　　　γ/F={L⊆{0,1}*|∃B∈γ,h∈F,L=｛x｜<x,h(|x|)>∈B}

これは、非常にややこしいのですが慣れて頂くほかなく、まず、L=｛x｜<x,h(|x|)>∈B}によってBが規定され、そのうちの∃Bを元とするという事で
が規定されています。なんだこりゃですね。

こうしてみると、<x,h(|x|)>が与えられればxは簡単に計算できます。すなわち、この場合h(|x|)が助けを与えているわけですが、そういう余分な情報を<x,h(|x|)>は持っていると見なせるということになります。

さて、このような場合

　γ＝P, F=Poly

のP/Polyが重要になってくるということで、次回からはこの解説になります。

サーキットの計算量の様々なクラス その6

おはようございます。「一粒で何度もおいしいこの冒頭の云々」と前回書いたところ非常に微妙な反応がありましたので、一粒で何度も微妙な味わいのあるこの冒頭のつかみの部分とお詫びして訂正させて頂きたいと思います。


さて、今回まではユニフォームのクラスについてもう少しお話しすることになります。

ここまで、論理式やサーキットの計算量のクラスがなんであるかと言うことを考えていましたが、今度は逆にクラスPをサーキットで表わすということについて考察していきます。

再びTM（チューリングマシンの略、以下同じ）のインプットがx、n=|x|として処理時間がt(n)、空間量がs(n)であるようなプログラムMの場合を考えます。

前にも言いましたが、プログラムはすべてコーディングして自然数に表せますし、ご存じの通りコンピュータの中ではすべてが二進数で表わされていますので、結局|x|=nなるxは、nビットの0と1で表わされる二進数の元を持つ集合{0,1}^n(※)の元ということにもなります。

※注：{0,1}^nの　^nの部分はべき乗を表わす数字のように右肩に乗るようなものですが、便宜上、以下このように表わしていきます)

このような場合、言語LがTMのプログラムMで決定されるとすると以下のような定理がなり立つという事になります。

「プログラムMで決定される言語LはサイズがO(t(n)log s(n))のサーキットで表わされる」
（※註：テキストでも証明は省略されており、参考文献があります。「I.Wegener, The complexity of Boolean Functions, John Wiley and Teubner,1987 pp.271-277」）

この定理は要するに、クラスP は多項式サイズのサーキットによって計算可能ということになります。当然と言えば当然ですけど、結構これも難しい証明があるようですね。

もう少し考察を進めると、ここまで、多項式サイズのサーキットであっても計算量がクラスPであるためにはユニフォームという条件が必要だということでお話をしていました。言い換えれば、クラスPはユニフォームな多項式サイズのサーキットで表わされる言語全体と言うこともつまりそう定義することも可能ということになります。

さて、ここからはテキストを引用して終わりましょう。一部前回引用した部分も含みます。

「（上のようにクラスPがユニフォームな多項式サイズのサーキットで表わされる言語全体と定義できると言うことは）NC^1とPとの関係において重要である。すなわちNC^1は多項式サイズの論理式、Pは多項式サイズのサーキットということになる。この意味ではNC^1はPの純粋な部分という気分がする。したがってPについての問題はNC^1にあてはめてまず考えるのが良いと思う。特にP=NPの問題のためには、まず

　NC^1≠AC^1

をかんがえ、解決するのが本質に迫る方法の一つだと思う」

サーキットの計算量の様々なクラス その5

おはようございます。一粒で何度でもおいしいこの冒頭のつかみの部分。実はこの部分が一番時間と労力を使っているのでは無いかと思われるというのは内緒です。いや、しかし、よく考えればそれこそP=NP問題。テキストに書かれている部分は分っている事実ですので計算量はクラスP ですからね。だから難しくないか、といえばそうでもないところが、この世の深淵に触れる一事実というべきなのでしょうか。


さて、前回は、ノンユニフォームを考える場合の制限とPSPACE、LSPACE（この記事ではLとも表記される）について少し触れました。空間についての計算量の考察は、

　L⊆P

　L≠PSPACE

　NC^1⊆LSPACE⊆AC^1

が前回挙げられた証明済みの関係ですが、ユニフォームの制限がある場合、一般に、

　NC^0⊆AC^0⊆NC^1⊆AC^1⊆NC^2⊆AC^2⊆………⊆NC=AC⊆P

という事が成り立ちますから、LSPACEをLと表わすと

　　NC^0⊆AC^0⊆NC^1⊆L⊆AC^1⊆NC^2⊆AC^2⊆………⊆NC=AC⊆P

という事は容易に分かると思います。しかし、この包含関係のイコールの部分が成立するかどうかについては、一般には成立しないと思われているようですが、この予想で証明があるのは、

　AC^0≠NC^1

だけという大変難しい問題のようです。

竹内先生におかれましては、このあと、P=NP問題については、


「
　NC^1≠AC^1

を考え解決するのが本質に迫る方法の一つと思う」(テキストp.47)


と書かれています。これについては追々説明していくということで、まず、ノンユニフォームでの場合のNC^1についてもう少し分っている事実などを述べていきたいと思います。

NC^1について、多項式このインデグリーを2に直すのに必要な計算量はO(log n)になることは自明だと思います。次に多項式個のアウトデグリーを1個のアウトデグリーに変換するには多項式時間で済むという事になります。言い換えると、NC^1は多項式サイズの論理式に変換することができるでしょう。

ところで、証明は省略しますが、Spiaの定理というものがスレッシュホールド関数を扱う場合分っている事実として証明されていますので、これを使うと、NC^1は多項式サイズで深さがO(log n)の論理式で表わされるという事が分かるということになるようです。

「このようなNC^1の定式化はNC^1の内容を良く表わす上で重要である」(テキスト p46)

と竹内先生は書かれていますので、ご紹介しておきます。

サーキットの計算量の様々なクラス その4

おはようございます。ではなく、今日はになってしまいました。団体競技だとユニフォームがありますよね。無いと何となく締まらない感じがするのは私だけでしょうか。しかし、学校の制服となるとどうなんでしょうね。そういうふうに、いろいろ悩ましいユニフォームですが、サーキットのクラスにおいてもなかなか悩ましく、いやいや、だからって何もない方が良いって事じゃ無いんですけどね。

今回はノンユニフォームの場合を考えると言うことでした。

まず、現在考えている族{C1,C2,…}で表わされたサーキットや論理式がサイズにおいてが多項式サイズであるという制限を外すとどうなるかというと、インデグリー1であってもチューリングマシンでの計算自体は多項式時間で終わらない可能性のあるものはいくらでも考えられますので、そういうものは計算不可能すなわちクラスPには入らないということになります。

そこで、NC^iやAC^iについて考えるときユニフォーム即ち以下の定義を「サーキットの計算量の様々なクラス　その2」示していますが


【ユニフォームの定義】
ある種の族{C1,C2,…}で表わされたサーキットや論理式などを自然数に置換し、置換した自然数を再び同じ族で表わすことができるとする。このとき

　f(i)=Ci　

という関数があって、それをクラスAC^0で表わすことができるもの



この制限を廃したNC^iやAC^iについて考える、という事になります。

これがこれからの流れにおいて考慮に入れておく点ですが、その他いくつかこれまで省略しておいたPSPACEというものを補足したいと思います。

まず、現在TM（以下チューリングマシンをこう表記する）で多項式時間で解けるかどうかがクラスPに入る問題かどうかと言うことでインプットxに対しn=|x|としたときの時間t(n)をもっぱら扱ってきましたが、一方でTMのヘッドの動く距離（あるいはテープの動く距離）が有限であるかどうか問うことも問題となるということを「クラスPとチューリングマシンその2」）においても簡単に触れていました。ここでは、その空間的な量をs(n)と表わすことにし、その量が多項式で表せるものを多項式空間PSPACEとします。

ところで、ヘッドはテープの同じ場所を何度も訪れることができるために、一般に

　P⊆PSPACE

であることは容易に分ります。

ところで、多項式空間では無く、TMのプログラムがO(log n)で必ず停止し受容されると言うようなプログラムのクラスもあります。これはLOGSPACEもしくはLSPACEで表わされ、時には単にLと書かれる場合もあります。

LとPの関係は

　L⊆P

となっているようですが、はっきり証明があって分っているのは

　L≠PSPACE

そして、

　NC^1⊆LSPACE⊆AC^1

などで、分っていないことがかなり多いとテキストには書かれています。

サーキットの計算量の様々なクラス その3

およげたいやきくんではありませんが、まいにちまいにち、鉄板の穴の中でくるくると回されながら焼かれている気がしている今日この頃。今朝もくるくると早朝から働かせていただいております。

さて、今回はNC^iとAC^iの包含関係などを検討していくことになります。

テキストによると、このような議論をするときユニフォームとは限らないサーキットの族Cnが、多項式のサイズで深さが

であると考えます。

ところで、NC^iのインデグリーが定数で抑えられているのに対してAC^iはなんの制限もありませんので一般的に、

　NC^i⊆AC^i

であることは明らかです。

次に、NC^iのインデグリーを抑えている定数をcとするときインデグリーcのサーキットをインデグリーが0か2のバイナリーサーキットに置き換える事を考えると、このことは可能であることもサーキットのサイズsはlogc倍増えるであろう事は簡単に分ります。

ところで、

　AC^i⊆NC^i+1

を検討してみると、これは定義からして深さはO(log n)倍、サイズもこの記事の最初に定義したように多項式倍に増える、という事になるだけと言えます。

ここで、

　NC=∪NC^i,　AC=∪AC^i

とすると、以上より

　NC=AC

ということが言え、NCやACにはユニフォームという制限、即ち、自己言及可能であるという制限がついていますので

　NC=AC⊆P

が言えるということになります。すなわち、たいていのサーキットはチューリングマシンで計算可能であると言える、という事になります。

今回はここまでです。次回からはNCとACのユニフォームという制限を外した場合、即ちノンユニフォームなサーキットでの場合をしばらく考えるということになります。

サーキットの計算量の様々なクラス 補足1

前回の補足を少しさせて頂きたいと思います。

NC^i,AC^iの定義で、

ユニフォームなサーキットの族{Cn1,Cn2,…}で、多項式のサイズや深さが




という事をお話ししましたが、まず、どうしてこのようなことをやるのかということについて、テキストには書いてありませんが、私の思うところを少しお話ししたいと思いいます。

まず、このブログの3回目に「集合論における整数」という記事で簡単に整数や実数の無限に触れ、濃度という考え方を説明しています。今回はそれにも関係することです。

少し視野を広げてみると現在やっていることは数学基礎論（Wikipedia：http://ja.wikipedia.org/wiki/数学基礎論　を参照のこと）という分野でやっていることにあたります。数学基礎論とは数学の分野ではありますが、比較的新しい分野で、数学自体の基礎を数学によって表現できるか、その限界や方法論を扱っている分野でもあります。

どうでも良いですが、高校三年生の数Ⅲで習う微分方程式などは、フーリエ変換=>ラプラス変換という具合にして代数的に求める方法というのが確立されています。量子力学でももっぱらこういうものを使って軌道の非連続性の説明していたと記憶していますが、どうにも自分が知らないことはどうでも良い事だというように仰る方もいらっしゃるようですので、少し書いてみました。

さて、話を

について戻すと、実数の無限大をωとして扱うと、このωを一つの数として考えて、

　ω，2ω，…

となどどんどん数を増やしていき、ωのω個というのを




　

というように表記します。

サーキットは論理式で表わされ、考えられる論理式を整数に一対一で対応させるようなことを考えると、




というのが、じつは






に対応しているのではないかということは誰の目にも明らかでしょう。


さらに、このように論理式を一対一に対応する整数で表わす（以下これを整数でコーディングすると呼びます）が、この考え方は、ゲーデルが不完全性定理を証明するときに用いた考え方であり、自分自身が正しいかどうかを証明するのには自分自身で証明することはできないという考え方に用います。そういうことから、数学の特に整数を扱う部分への公理系への洞察がなされるという事になります。今回の節の最後に、言語について少し触れるかもしれませんが、ここでいいう言語というのは公理系の別名とも言えます。(どういう表記をするかということにも少し特徴がありますが）

サーキットの計算量の様々なクラス その2

しかし、どうしていじめというのは無くならないんですかね。私もんＨＫのいまはあれであれをああし続けてどうしているのか不明の方にタコだとか何とか言い続けられましたが、別にくねくねしたくてしているわけでも無し、なんでそういうことを言うかな、と思うわけですよ。要するに、気に入らないからといって何をしても良いと思っている人もたくさんいらっしゃって、こちらに原因がないとは言いきれないとは思いますがねえ。


　さて、計算量のクラスとしてNC^i、AC^iの説明に入りたいと思います。実は、

　NC^i


は


　


と

　AC^iは


　


と表記するのですが、これからたびたび説明で使う関係上、その度に図で表記するのも煩雑なのでNC^i、AC^iという表記を使わせて頂きたいと思います。多少見にくいですがどうぞご了承下さい。


まずは定義から

【NC^i,AC^iの定義】

ユニフォームなサーキットの族{C1,C2,…}で、多項式のサイズや深さが




で、NC^iはインデグリーが定数で抑えられているもの。AC^iは、インデグリーに制限のないもので計算されるブールの族。

［用語の解説］
※族：数学における族（ぞく、family）は、添字付けされた元（要素）の（一般には非可算無限個の）集まりで、対、n-組、列などの概念の一般化である。系（けい、collection）と呼ぶこともある。元がどのような対象であるかによって、点族、集合族（集合系）、関数族（関数系）などと呼ばれる。
　　（Wikipedia（http://ja.wikipedia.org/wiki/族_(数学)より引用））

※ユニフォーム：定義としては、ある種の族{C1,C2,…}で表わされたサーキットや論理式などを自然数に置換し、置換した自然数を再び同じ族で表わすことができるとする。このとき

　f(i)=Ci　

という関数があって、それをクラスAC^0で表わすことができるもの



今回はもう少しこの定義について解説したあと、次回以降、それぞれのクラスの包含関係などの考察に入ります。

今まで考察してきたもののサイズや深さはO(log n)でした。即ちこれが現時点ではもっとも一般的に有用なグラフといえるかもしれません。ところが、これはいま平面上にサーキットがあったから、そうだとも言えます。これが立体面であれば、オーダーはこの自乗になるのは自明です。そのように次元を上げていった場合などを一般化して扱うのが数学とも言えます。そういうわけで今回は、



の場合、すなわちNC^i,AC^iの場合も考察してみようということになるわけです。

サーキットの計算量の様々なクラス その1

一難去ってまた一難といった様相を見せる私の立場。台風のあとは相場が大荒れで、といっても貧乏な私にはあんまり関係ないはずのですが、最近ほんのちょっぴり勉強がてら投資したら、もう下がるわ下がるわ、びっくりするほど下がり続けて、本当に良い勉強になっている今日この頃。やっぱり秋は学問の秋ですかねえ。え、なんかちがいますか。

さて、前節では、基本的に二分木の場合を前提としていました。実は私も忘れていたのですが、「サーキットというグラフ　その1」にて、サーキットの定義として以下のことを書いているのでした。

【サーキットの定義】
　いま、ブール変数x1 , … , xnが与えられているとします。グラフは、無サイクルな有方向グラフであり、
　　
　　（１）すべてのノードのインデグリーは0、もしくは、2である
　　　　（１－１）インデグリー0のノードをインプットもしくはリーフと呼ぶ
　　　　　　　　　（一般に、入力であるブール変数x1 , … , xn が相当する）
　　　　（１－２）インデグリー2のノードはゲート（gate）と呼ばれ
　　　　　　　　　∧（論理積）もしくは∨（論理和）が付加されている
　　（２）アウトデグリーの値は任意であるが、アウトデグリー0のノードが
　　　　　ただ一つだけあり、このノードのことをアウトプット(output)と呼ぶ
　
以上を満たすものをこれから、ブール変数x1 ,…, xn 上のブーリアン・サーキット（Boolean circuit）または、単にサーキットと呼ぶことにします。

何せ、ソチオリンピックよりも前のこと。忘れていても仕方ないですが、もうすぐ一年にもなろうとしていますから月日の経つのは本当に早いですね。


さて、今回からは、このインデグリーが0か2という制限を外していろんなインデグリーの数の場合のことを考えていくことになります。即ち、一つのゲートの論理式が

もしくは

　


ということもあるということです。こうしたとき、バイナリーサーキットから上の形式のノードをいくつか用いる形で書き直すこともできます。そのようにして論理式Fを書き直してできる同様の論理式をF'としたときもリーフの数は変わりませんので

　L(F)=L(F')

となりますね。このように途中のノード（ゲート）を集約してもしてもサイズ（リーフの数や深さ）は変わらないのが一般的です。そこができるのであれば、そもそもの論理式に無駄があったということになります。

余談ですが、主に電子回路ではこのようなノードのことをゲートと呼びます。すなわち、真であれば電流が流れ、あるいは電圧が印加される部分の関門というイメージだと思われます。以下、テキストも拡張したゲートをノードと区別せずに単にゲートと呼んでいますので、ややこしいですがこの節では、それらも単にゲートと呼ぶことします。

さて、今言ったことをもう少し数学的に考えてみましょう。


サイズs:サーキットCがあったときのCのサイズとし,Cの中のゲート数をs(C)という形で表わす


というように定義します。

このとき、当然s(C)≠L(C)ですが、かりにサーキットCが二分木のようなバイナリーサーキットであるとすれば、

　s(C)=L(C)-1

として定義できるのはちょっと考えれば分ります。面白いので是非ご自分で考えて下さいね。

さらにサーキットCは論理式Fと等価であることからs(C)はs(F)という形でも表わされ、当然、

　s(F)=L(F)-1

となります。

今回はこのあたりで。

次からは本格的にクラスの定義に入っていきます。

サーキットというグラフの計算量 その6

さて、またどういうわけか朝からがんばっていますが、さすがに来週は台風さんの来襲も無いようで、ほっと一息ついています。もう、本当に申し訳ありません、とわけも分からぬ自責の念に駆られてしまい謝りたくなるほどの台風の襲来でありました。


さて、前回は、

を求めましたが、今回は


　　　L(Parity(x1,x2,…,x2n))≦4・L(Parity(x1,x2,…,xn))


という事から

　　　

という事を求め、合わせ技で

ということを説明します。


まず思い出して頂きたいのは、


￢Parity(x1,x2,…,xn)=1-Parity(x1,x2,…,xn)

　※厳密には￢は否定演算子で、単なる否定は式にアッパーラインが引いてあるものが正式ですがここでは区別していません


という式。これは、「サーキットというグラフの計算量　その２」で説明しているのですが、要するに結果として0と1が、1と0に反転するという岳ですので、二分木にしても大きさが変わるわけでは無いという、それだけ簡単に納得して頂ければいいわけです。二分木の図を書いても良いのですが、単にリーフ0と1の出力を逆になるように否定を取るだけ良いだけですので省略です。


　　　L(Parity(x1,x2,…,xn))＝L(￢Parity(x1,x2,…,xn)）


ここで、Parityの二分木の例を再掲しますと

Parityの二分木の例

となりますが、この図からも分りますように



　　　Parity(x1,x2,…,x2n))

　　　　　⇔[{Parity(x1,x2,…,xn)∧￢Parity(xn+1,xn+2,…,x2n)}
             ∨{￢Parity(x1,x2,…,xn)∧Parity(xn+1,xn+2,…,x2n)}]

　　　　　⇔[{Parity(x1,x2,…,xn∨Parity(xn+1,xn+2,…,x2n)}
             ∧{￢Parity(x1,x2,…,xn)∨￢Parity(xn+1,xn+2,…,x2n)}]

　　　　　　　※⇔は同値を表わす


ですので、一般的には、


　　　L(Parity(x1,x2,…,x2n))≦4・L(Parity(x1,x2,…,xn))


が言え、これをどんどん展開していくと


　　　L(Parity(x1,x2,…,x2n))≦4・L(Parity(x1,x2,…,xn))
　　　　　　　　　　　　　　　≦4・４・L(Parity(x1,x2,…,xn/2))
　　　　　　　　　　　　　………
　　　　　　　　　　　　　　　≦（ただし上の例図のようにn=2のd乗で表せるとする）


という事になります。

したがって、前回求めた


　　


と合わせて考えると

　　

という事になります。


以上で、ここでサーキットというグラフ計算量のお話はいったん終わらせて頂きます。テキストではこのあとスレッシュホールド関数の計算量の話が少し出てきているのですが、詳しいことは分っていないということで、Krapchenkoの定理を利用して分っている範囲での事に少し触れてありますが、省略したいと思います。基本的にはどういうことをやっているのか、ということをここでは理解して頂ければ十分だと思うからです。興味のある方は、個別に私宛にご連絡頂ければ、ご相談に応じることはやぶさかではありません。



次回からは「このブログを再開するに当たってのこれからの進め方」の回でお話ししている、


　２－２．サーキットの計算量の様々なクラスを考察する


という事に入っていこうと思います。そのあと


　２－３．ユニフォームという概念


ということを説明し、

　　３．モノトーン（否定のリテラルがない論理式）のサーキットが

　　　　多項式時間以内で解けない問題であることを証明する

というところで、再びサーキット（この場合はモノトーンサーキットになりますが）の計算量に関してはじっくり考察することになります。

サーキットというグラフの計算量 その5

今日も今日とて早朝からがんばっていますが、何となく台風上陸との報に罪悪感を感じてしまう私。関係ないのは分っているのですが。と、とにかく、被害の無いことをお祈りするのみです。


前回はKhrapchenkoの定理の証明を証明しました。今回はこれを用いて、以下の命題を証明するということの説明を行います。






まず、AとBとが２値0か1を元とし、n個の元を持つ集合{0,1}^nの互いに素な部分集合だったという事を思い出して下さい。さらに、今回は以下のようにその互いに素な集合を定義すると

　A={(x1,x2,…,xn)|Parity(x1,x2,…,xn)|=0}
　B={(x1,x2,…,xn)|Parity(x1,x2,…,xn)|=1}

論理式parity(x1,x2,…,xn)が集合Aと集合Bを分離しているのは明らかです。また、

　

　　　 　　　　　　　　※AとBの元はそれぞれのnビット。
　　　　　　　　　　　　　ゆえににAとBの1ビットの差異は
　　　　　　　　　　　　　
　　　　　　　　　　　　　n個×（集合A(もしくはB)の元の個数）


なので、これをKhrapchenkoの定理

に代入してやると求める命題

が出てくるということになります。


意外と簡単に出てくるものですね。頭のいい人の考えることは本当に違いますねえ。

さて、次は

　　　L(Parity(x1,x2,…,x2n)|)≦4・L(Parityx1,x2,…,xn))

という事から

　　　L(Parityx1,x2,…,xn))≦(nの2乗)

という事を求め、今回求めた

　　　L(Parityx1,x2,…,xn))≧(nの2乗)

と合わせ技で

　　　L(Parityx1,x2,…,xn))＝(nの2乗)

ということを説明します。(nの2乗)を




としなかったのは単に説明上の都合です。面倒だからじゃ無いですってば。

サーキットというグラフの計算量 その4

秋になって、どういうわけかやる気が起こってきたのか、何となくがんばっている私。この時期になっても台風がいくつも来るわけだ、と個人的には納得してはいけないことも納得してしまいそうな今日この頃。皆様はなんの秋でいらっしゃいますでしょうか。

そういうわけで、ってどういうわけか知りませんが、最近早朝からがんばっている私。しかし、このブログ誰が読んでいるんでしょうねって自分でいったらいけないか。

今回はKhrapchenkoの定理の証明ですね。注意しておきますと、これは、パリティのリーフの数を計算すつと言うよりもう少し一般的な定理になり、この定理からパリティのリーフが求まるという順序になります。

再掲すると、

AとBとが集合{0，1}^n（0と1の元をn個持つ集合）の互いに素な部分集合だとするとき論理関数FがAとBとを分離することを、Aに対してはFが0、Bに対してはFが1となることと定義する。また、このようなとき、以下のことを定義していると、


つぎの式が成り立つ、

　　

という事でした。


以下証明です。

【Khrapchenkoの定理の証明】

数学的帰納法により次のように証明していきます。

上の式が成り立つと仮定します。


(i)　L(F)（リーフ）が1のとき
　まずL(F)=1のときの例としてF(x1,x2,…,xn)=x1となるような式を考えます。このときa～bという式は、仮にa=(0,a2,…,an)であるならばb=(1,a2,…,an)であるという事と同等になります。したがって以下のことが言えることとなり、

が成立。少し変形し、二つの式をお互いに掛け合わせれば容易に、

が導けます。


(ii)L(F)>1のとき
　F=F1∧F2とします。このときA1とA2とを次の式で定義することにします。
　
   　A1={a∈A|F1(a)=0},　　　A2=A-A1

すなわち、A1を論理関数F1でBから分離できるものだけにする、ということです。これをi回繰り返してみるとFiによってAiはBから分離できるということになり、帰納法の仮定より

という式が導き出せます。さらに、F=F1∧F2でしたからL(F)=L(F1)+L(F2)が成り立ちますから、

となります。ところで、

であることから

という式が成立することに。これは右辺が定理の右辺に相当しますから（左辺は定理の左辺より当然小さい）、従って数学的帰納法により、Khrapchenkoの定理が証明されました。上の式を変形するとこの式が成り立つことが分ります。つまり、上の式をひらめいたことがこの定理のキモということになるわけですよね。


というわけで次回は、Khrapchenkoの定理から

　　L(Parity(x1,…,xn))≧(nの2乗）

という式を証明します。上の式で(nの2乗）としてきちんと式を図にして表示していないのは、今回関係ないところだったからで、次はきちんとします。単に面倒だったから、とかそう言うわけではありません。多分………。

サーキットというグラフの計算量 その3

いろいろあって、半年に一本というペースに落ちてきていますが、誰かのせいです。どいつだー。いえ、すべて私のせいなんですが。人間誰しも自分が悪すぎて恥ずかしいときには他人のせいにしたくなりますよね。特に怖い人の前では。幸い私には奥さんがいませんけれども、私の怖い人にはいらっしゃるだろうということで、やはり奥さんは大切にしないといけません。

えっと、なんだか訳が分らなくなってきましたが、話しを続けさせて頂こうと思います。

今回からしばらくは、パリティを計算するようなグラフが持つリーフの数L(Parity)についてお話しします。パリティの基本的な性質をグラフの計算量の例としてて説明するということが主な目的です。これが分ると自然と深さd(Parity)も分ります。

まず、パリティを計算する場合の論理式Fをグラフにしたものの例を下に示します。ブール変数はx1,x2,x3,x4の4ビットですが、リーフL(F)=16,深さd(F)=4となっています。ここからしばらくは、このようなグラフのリーフの数L(parity)の求め方を説明します。

図　 parity関数の例

ちなみにこういうグラフの形を二分木と呼んだりもします。そして一番上のノードを根（root）と呼びます。根からリーフまですべてのノードは下のノードからインプットとして二つの枝を持ちます。そのため二分木と呼ばれるわけです。このようなグラフの深さは必ずd=logL(F)（ただし対数の底は2）となることは自明ですね。ちなみに計算機科学などの計算機を扱う分野では対数の底は特に断らない限り2です。これは計算機の世界が基本的に2進数で物事を表現することが基本だからです。ここでも特に断らない限り以下、対数の底は2ですのでご注意下さい。

今回はまず、準備として以下のことを定義しておきます。

元が0と1からなり、n個の元を持つ集合を{0,1}^nと表記することにします。この集合｛0,1}^nの部分集合で互いに素である二つの集合ＡとＢを論理式Ｆが分離するという事を定義して、FがＡの元に対しては0、Ｂの元に対しては1を取るという事にします。

また、部分集合ＡとＢに対して以下のことを定義します。

このあとはKhrapchenkoの定理と呼ばれる次の不等式を帰納法で証明します。それは次回に。できる方は自分で証明を考えてみると面白いかもしれません。