さて、またどういうわけか朝からがんばっていますが、さすがに来週は台風さんの来襲も無いようで、ほっと一息ついています。もう、本当に申し訳ありません、とわけも分からぬ自責の念に駆られてしまい謝りたくなるほどの台風の襲来でありました。
さて、前回は、

L(Parity(x1,x2,…,x2n))≦4・L(Parity(x1,x2,…,xn))
という事から
という事を求め、合わせ技で
ということを説明します。
まず思い出して頂きたいのは、
¬Parity(x1,x2,…,xn)=1-Parity(x1,x2,…,xn)
※厳密には¬は否定演算子で、単なる否定は式にアッパーラインが引いてあるものが正式ですがここでは区別していません
という式。これは、「サーキットというグラフの計算量 その2」で説明しているのですが、要するに結果として0と1が、1と0に反転するという岳ですので、二分木にしても大きさが変わるわけでは無いという、それだけ簡単に納得して頂ければいいわけです。二分木の図を書いても良いのですが、単にリーフ0と1の出力を逆になるように否定を取るだけ良いだけですので省略です。
L(Parity(x1,x2,…,xn))=L(¬Parity(x1,x2,…,xn))
ここで、Parityの二分木の例を再掲しますと
 |
| Parityの二分木の例 |
となりますが、この図からも分りますように
Parity(x1,x2,…,x2n))
⇔[{Parity(x1,x2,…,xn)∧¬Parity(xn+1,xn+2,…,x2n)}
∨{¬Parity(x1,x2,…,xn)∧Parity(xn+1,xn+2,…,x2n)}]
⇔[{Parity(x1,x2,…,xn∨Parity(xn+1,xn+2,…,x2n)}
∧{¬Parity(x1,x2,…,xn)∨¬Parity(xn+1,xn+2,…,x2n)}]
※⇔は同値を表わす
ですので、一般的には、
L(Parity(x1,x2,…,x2n))≦4・L(Parity(x1,x2,…,xn))
が言え、これをどんどん展開していくと
L(Parity(x1,x2,…,x2n))≦4・L(Parity(x1,x2,…,xn))
≦4・4・L(Parity(x1,x2,…,xn/2))
………
≦
 (ただし上の例図のようにn=2のd乗で表せるとする)
(ただし上の例図のようにn=2のd乗で表せるとする)という事になります。
したがって、前回求めた

と合わせて考えると
以上で、ここでサーキットというグラフ計算量のお話はいったん終わらせて頂きます。テキストではこのあとスレッシュホールド関数の計算量の話が少し出てきているのですが、詳しいことは分っていないということで、Krapchenkoの定理を利用して分っている範囲での事に少し触れてありますが、省略したいと思います。基本的にはどういうことをやっているのか、ということをここでは理解して頂ければ十分だと思うからです。興味のある方は、個別に私宛にご連絡頂ければ、ご相談に応じることはやぶさかではありません。
次回からは「このブログを再開するに当たってのこれからの進め方」の回でお話ししている、
2-2.サーキットの計算量の様々なクラスを考察する
という事に入っていこうと思います。そのあと
2-3.ユニフォームという概念
ということを説明し、
3.モノトーン(否定のリテラルがない論理式)のサーキットが
多項式時間以内で解けない問題であることを証明する
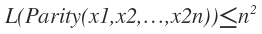
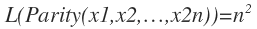
0 件のコメント:
コメントを投稿
Etsuro.Honda@futarisizuka.org